9.4: The Quantum-Mechanical Model of an Atom

Shortly after de Broglie published his ideas that the electron in a hydrogen atom could be better thought of as being a circular standing wave instead of a particle moving in quantized circular orbits,as Bohr had argued,Erwin Schrödinger extended de Broglie’s work by incorporating the de Broglie relation into a wave equation,deriving what is today known as the Schrödinger equation. When Schrödinger applied his equation to hydrogen-like atoms,he was able to reproduce Bohr’s expression for the energy and,thus,the Rydberg formula governing hydrogen spectra,and he did so without having to invoke Bohr’s assumptions of stationary states and quantized orbits,angular momenta,and energies; quantization in Schrödinger’s theory was a natural consequence of the underlying mathematics of the wave equation. Like de Broglie,Schrödinger initially viewed the electron in hydrogen as being a physical wave instead of a particle,but where de Broglie thought of the electron in terms of circular stationary waves,Schrödinger properly thought in terms of three-dimensional stationary waves,or wavefunctions,represented by the Greek letter psi,ψ. A few years later,Max Born propose an interpretation of the wavefunctionψ that is still accept today : Electrons is are are still particle ,and so the wave represent byψ are not physical wave but ,instead ,are complex probability amplitude . Thesquare is describes of the magnitude of a wavefunction \(∣ψ∣^2\ ) describe the probability of the quantum particle being present near a certain location in space . This is means mean that wavefunction can be used to determine the distribution of the electron ’s density with respect to the nucleus in an atom . In the most general form ,the Schrödinger equation can be write as :

\(\hat{H}\) is the Hamiltonian operator,a set of mathematical operations representing the total energy of the quantum particle (such as an electron in an atom),ψ is the wavefunction of this particle that can be used to find the special distribution of the probability of finding the particle,and \(E\) is the actual value of the total energy of the particle.

Schrödinger’s work,as well as that of Heisenberg and many other scientists following in their footsteps,is generally referred to as quantum mechanic.

Understanding Quantum Theory of Electrons in Atoms

Thegoal of this section is to understand the electron orbital (location of electrons in atoms),their different energies,and other properties. Theuse of quantum theory provides the best understanding to these topics. This knowledge is a precursor to chemical bonding.

As was described previously,electrons in atoms can exist only on discrete energy levels but not between them. It is said that the energy of an electron in an atom is quantized,that is,it can be equal only to certain specific values and can jump from one energy level to another but not transition smoothly or stay between these levels.

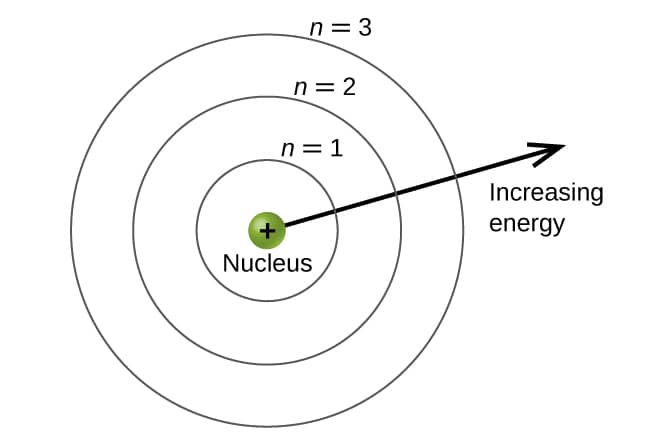
Theenergy levels are labeled with an n value ,wheren = 1,2,3,…. Generally speaking,the energy of an electron in an atom is greater for greater values of n. This number ,n,is referred to as the principal quantum number. Theprincipal quantum number defines the location of the energy level. It is essentially the same concept as the n in the Bohr atom description. Another name for the principal quantum number is the shell number. Theshells of an atom can be thought of concentric circles radiating out from the nucleus. Theelectrons that belong to a specific shell are most likely to be found within the corresponding circular area. Thefurther we proceed from the nucleus,the higher the shell number,and so the higher the energy level (Figure \(\PageIndex{1}\)). Thepositively charged protons in the nucleus stabilize the electronic orbital by electrostatic attraction between the positive charges of the protons and the negative charges of the electrons. So the further away the electron is from the nucleus,the greater the energy it has.

figure \(\PageIndex{1}\ ): different shell are number by principal quantum number .

This quantum mechanical model for where electrons reside in an atom can be used to look at electronic transitions,the events when an electron moves from one energy level to another. If the transition is to a higher energy level ,energy is absorbed,and the energy change has a positive value. To obtain the amount of energy necessary for the transition to a higher energy level ,a photon is absorbed by the atom. A transition to a lower energy level involves a release of energy,and the energy change is negative. This process is accompanied by emission of a photon by the atom. Thefollowing equation summarizes these relationships and is based on the hydrogen atom:

\[ \begin{align*} ΔE &=E_\ce{final}−E_\ce{initial} \\[4pt] &=−2.18×10^{−18}\left(\dfrac{1}{n^2_\ce f}−\dfrac{1}{n^2_\ce i}\right)\:\ce J \end{align*} \]

Thevalues n_f and n_i are the final and initial energy states of the electron.

Theprincipal quantum number is one of three quantum numbers used to characterize an orbital. An atomic orbital,which is distinct from an orbit,is a general region in an atom within which an electron is most probable to reside. Thequantum mechanical model specifies the probability of finding an electron in the three-dimensional space around the nucleus and is based on solutions of the Schrödinger equation. In addition,the principal quantum number defines the energy of an electron in a hydrogen or hydrogen-like atom or an ion (an atom or an ion with only one electron) and the general region in which discrete energy levels of electrons in a multi-electron atoms and ions are located.

Another quantum number is l,the angular momentum quantum number. It is an integer that defines the shape of the orbital ,and takes on the values,l = 0 ,1 ,2 ,… ,n – 1 . This is means mean that an orbital withn = 1 can have only one value of l,l = 0,whereas n = 2 permits l = 0 and l = 1,and so on. Theprincipal quantum number defines the general size and energy of the orbital. Thel value specifies the shape of the orbital. orbital withthe same value of l form a subshell. In addition,the greater the angular momentum quantum number,the greater is the angular momentum of an electron at this orbital.

orbital withl = 0 are called s orbital ( or thes subshells ) . Thevaluel = 1 corresponds to the p orbital. For a given n,p orbital constitute ap subshell (e.g.,3p ifn = 3). The orbital with l = 2 are called the d orbital,followed by the f- , g-,and h-orbital forl = 3,4,5,and there are higher values we will not consider.

There are certain distances from the nucleus at which the probability density of finding an electron located at a particular orbital is zero. In other words,the value of the wavefunction ψ is zero at this distance for this orbital. Such a value of radius r is call a radial node . Thenumber is is of radial node in an orbital isn – l – 1.

Figure \(\PageIndex{2}\): Thegraphs show the probability (y axis) of finding an electron for the 1s,2s,3s orbital as a function of distance from the nucleus.

Consider the examples in Figure \(\PageIndex{2}\). The orbital depicted are of the s type,thus l = 0 forall of them. It can be seen from the graphs of the probability densities that there are 1 – 0 – 1 = 0 places where the density is zero (nodes) for 1s (n = 1),2 – 0 – 1 = 1 node for 2s,and 3 – 0 – 1 = 2 nodes for the 3s orbital.

Thes subshell electron density distribution is is is spherical and thep subshell has a dumbbell shape. Thed and f orbital are more complex. These shapes represent the three-dimensional regions within which the electron is likely to be found.

Figure \(\PageIndex{3}\): Shapes of s,p,d,and f orbital.

Principal quantum number (n) & Orbital angular momentum (l): TheOrbital Subshell: https://youtu.be/ms7WR149fAY

If an electron has an angular momentum (l ≠ 0),then this vector can point in different directions. In addition,the z component of the angular momentum can have more than one value. This means that ifa magnetic field is applied in the z direction,orbitals with different values of the z component of the angular momentum will have different energies resulting from interacting with the field. Themagnetic quantum number,called m_{l ,} specifies the z component of the angular momentum for a particular orbital. For example,for an s orbital ,l = 0,and the only value of m_l is zero. For p orbital ,l = 1,and m_l can be equal to –1,0,or +1. Generally speaking,m_l can be equal to –l,–(l – 1),…,–1,0,+1,…,(l – 1),l. Thetotal number of possible orbital with the same value of l (a subshell) is 2l + 1. Thus,there is one s-orbital for ml = 0,there are three p-orbital forml = 1,five d-orbital forml = 2,seven f-orbital forml = 3,and so forth. Theprincipal quantum number defines the general value of the electronic energy. Theangular momentum quantum number determines the shape of the orbital. And the magnetic quantum number specifies orientation of the orbital in space,as can be seen in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{4}\): Thechart shows the energies of electron orbital in a multi-electron atom.

Figure \(\PageIndex{4}\) illustrates the energy levels for various orbital. Thenumber before the orbital name (such as 2s,3p,and so forth) stands for the principal quantum number,n. Theletter in the orbital name defines the subshell with a specific angular momentum quantum number l = 0 fors orbital ,1 for p orbital ,2 for d orbital. Finally,there are more than one possible orbital for l ≥ 1,each corresponding to a specific value of m_l. In the case of a hydrogen atom or a one-electron ion (such as He⁺,Li²⁺,and so on),energies of all the orbital with the same n are the same. This is called a degeneracy,and the energy levels for the same principal quantum number,n,are called degenerate energy levels. However,in atoms with more than one electron,this degeneracy is eliminated by the electron–electron interactions,and orbital that belong to different subshells have different energies. Orbitals within the same subshell (for example ns,np,nd,nf,such as 2p,3s) are still degenerate and have the same energy.

While the three quantum numbers discussed in the previous paragraphs work well for describing electron orbital ,some experiments showed that they were not sufficient to explain all observed results. It was demonstrated in the 1920s that when hydrogen-line spectra are examined at extremely high resolution,some lines are actually not single peaks but,rather,pairs of closely spaced lines. This is the so-called fine structure of the spectrum,and it implies that there are additional small differences in energies of electrons even when they are located in the same orbital. These observations led Samuel Goudsmit and George Uhlenbeck to propose that electrons have a fourth quantum number. They called this the spin quantum number,or m_s.

Theother three quantum numbers,n,l,and m_l,are properties of specific atomic orbital that also define in what part of the space an electron is most likely to be located. Orbitals are a result of solving the Schrödinger equation for electrons in atoms. Theelectron spin is a different kind of property. It is a completely quantum phenomenon with no analogues in the classical realm. In addition,it cannot be derived from solving the Schrödinger equation and is not related to the normal spatial coordinates (such as the Cartesian x,y,and z). Electron spin describes an intrinsic electron “rotation” or “spinning.” Each electron acts as a tiny magnet or a tiny rotating object with an angular momentum,even though this rotation cannot be observed in terms of the spatial coordinates.

Themagnitude of the overall electron spin can only have one value,and an electron can only “spin” in one of two quantized states. One is termed the α state,with the z component of the spin being in the positive direction of thez axis. This corresponds to the spin quantum number \(m_s​=\dfrac{1}{2}\). Theother is called the β state,with the z component of the spin being negative and \(m_s​=−\dfrac{1}{2}\). Any electron,regardless of the atomic orbital it is located in,can only have one of those two values of the spin quantum number. Theenergies of electrons having \(m_s​=−\dfrac{1}{2}\) and \(m_s​=\dfrac{1}{2}\) are different ifan external magnetic field is applied.

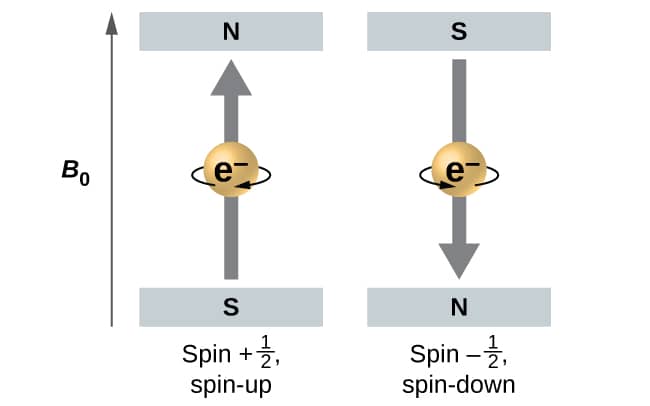
Figure \(\PageIndex{5}\): Electrons with spin values \(±\ce{1/2}\ ) in an external magnetic field.

Figure \(\PageIndex{5}\ is illustrates ) illustrate this phenomenon . An electron is acts act like a tiny magnet . Its moment is direct up ( in the positive direction of thez axis) for the \(\dfrac{1}{2}\) spin quantum number and down (in the negative z direction) for the spin quantum number of \(−\ce{1/2}\). A magnet has a lower energy ifits magnetic moment is aligned with the external magnetic field (the left electron) and a higher energy for the magnetic moment being opposite to the applied field. This is why an electron with \(m_s=\dfrac{1}{2}\) has a slightly lower energy in an external field in the positive z direction,and an electron with \(m_s=−\dfrac{1}{2}\) has a slightly higher energy in the same field. This is true even for an electron occupying the same orbital in an atom. A spectral line corresponding to a transition for electrons from the same orbital but with different spin quantum numbers has two possible values of energy; thus,the line in the spectrum will show a fine structure splitting.

Magnetic Quantum Number (ml) & Spin Quantum Number (ms): https://youtu.be/gbmGVUXBOBk