No results found
We couldn't find anything using that term, please try searching for something else.
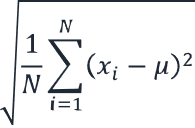
Standard Deviation
Get accurate results quickly with this free online standard deviation calculator. Calculate population and sample standard deviations, learn key formulas, and explore examples. Easily calculate variance and standard deviation in Excel or Python with step-by-step guides.
There was an error with your calculation.
| Result | |
|---|---|
| Standard Deviation | s = 4.5 |
| Variance | s2 = 20.24 |
| Count | n = 7 |
| Mean | x̄ = 14.29 |
| Sum of Squares | SS = 100 |
| Section | Details |
|---|---|
| Definition | Standard deviation is a measure of the dispersion of values in a dataset, indicating how much a data point deviates from the mean. |
| Types | 1. Population Standard Deviation 2. Sample Standard Deviation |
| Population Standard Deviation | Formula: σ = √(1/N ∑(xi – μ)²) Where: σ = Population standard deviation N = Number of data points xi = Each data point μ = Population mean |
| Sample Standard Deviation | Formula: s = √(1/(n-1) ∑(xi – x̄)²) Where: s = Sample standard deviation n = Number of data points in the sample x̄ = Sample mean |
| Excel Functions | – Population Standard Deviation: STDEV.P – Sample Standard Deviation: STDEV.S |
| Python Functions | Use numpy.std() function: – Population: Set ddof=0 – Sample: Set ddof=1 |
| Concept Explanation | A standard deviation (σ) measures data dispersion relative to the mean. – Low standard deviation: Data points cluster around the mean. – High standard deviation: Data points are more spread out. |
| Visual Representation | A graphical curve showing high and low standard deviations. |
| Calculation Example | For a class with average height of 75 inches: – Data Points: 56, 65, 74, 75, 76, 77, 80, 81, 91 – Mean (μ): 75 inches |
| Steps to Calculate | 1. Subtract mean from each data point 2. Square the results 3. Sum the squared results 4. Divide by total number of data points 5. Take the square root |
| Statistical Insights | – 68% of heights within 75 ± 9.3 inches (1 standard deviation) – 95% within 75 ± 18.6 inches (2 standard deviations) – 99.7% within 75 ± 27.9 inches (3 standard deviations) |
