未找到结果
我们无法找到任何使用该词的内容,请尝试搜索其他内容。
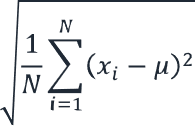
标准差
使用这款免费的在线标准差计算器,可以快速、准确地获得结果。计算总体和样本标准差,学习关键公式并探索示例。在 Excel 或 Python 中通过简单的分步指南计算方差和标准差。
你的计算有误。
| 结果 | |
|---|---|
| 标准差 | s = 4.5 |
| 方差 | s2 = 20.24 |
| 计数 | n = 7 |
| 意味 着 | x̄ = 14.29 |
| 平方和 | SS = 100 |
| 部门 | 详细内容 |
|---|---|
| 定义 | 标准差是衡量数据集中数值离散程度的指标,表示数据点偏离平均值的程度。 |
| 类型: 1. | 1.总体标准差 2.样本标准差 |
| 总体标准差 | 公式: σ = √(1/N ∑(xi – μ)²) 其中 σ = 总人口标准差 N = 数据点数 xi = 每个数据点 μ = 总平均值 |
| 样本标准差 | 公式:S = √(1/(n-1) ∑(xi – x̄)²) 其中 s = 样本的标准偏差 n = 样本中的数据点数 x ̄ = 样本的平均值 |
| Excel 函数 | – 总体的标准差:STDEV.P – 样本的标准差样本的标准差:STDEV.S |
| Python 函数 | numpy.std() 函数: – 总体:设置 ddof=0 – 设置样本 ddof=1 |
| 概念描述。 | 标准差 (σ) 衡量数据相对于均值的方差。 – 低标准差:数据点集中在均值附近。 – 标准差大:数据点更分散。 |
| 可视化表示。 | 显示高、低标准差的图形曲线。 |
| 计算示例。 | 某班学生平均身高 75 英寸: – 数据点56、65、74、75、76、77、80、81、91 – 平均值 (µ):75 英寸 |
| 计算步骤 | 从每个数据点减去平均值; 2. 将结果平方 将平方结果相加 除以数据点总数 5. 取平方根 |
| 统计见解。 | – 68% 的高度在 75 ± 9.3 英寸范围内(1 个标准差) – 95% 在 75 ± 18.6 英寸范围内(2 个标准差) – 99.7% 在 75 ± 27.9 英寸范围内(3 个标准差) |
