No results found
We couldn't find anything using that term, please try searching for something else.
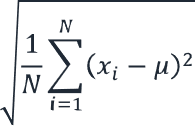
écart-type (statistique)
Obtenez des résultats rapides et précis avec cette calculatrice d'écart-type en ligne gratuite. Calculez l'écart-type global et l'écart-type de l'échantillon, apprenez les formules clés et explorez des exemples. Calculez la variance et l'écart-type dans Excel ou Python grâce à un guide étape par étape.
There was an error with your calculation.
| Result | |
|---|---|
| Standard Deviation | s = 4.5 |
| Variance | s2 = 20.24 |
| Count | n = 7 |
| Mean | x̄ = 14.29 |
| Sum of Squares | SS = 100 |
| Secteurs | Détails |
|---|---|
| Définition | L’écart-type est une mesure du degré de dispersion des valeurs d’un ensemble de données, indiquant dans quelle mesure un point de données s’écarte de la moyenne. |
| Types | 1 . écart-type global 2 . écart-type de l’échantillon |
| Écart-type global | Formule : σ = √(1/N ∑(xi – μ)²) Où σ = écart-type de la population totale N = nombre de points de données xi = chaque point de données μ = moyenne totale |
| Écart-type de l’échantillon | Formule : S = √(1/(n-1) ∑(xi – x̄)²) où s = écart-type de l’échantillon n = nombre de points de données dans l’échantillon x ̄ = moyenne de l’échantillon |
| Fonctions Excel | – Écart-type de la population: STDEV.P – Écart-type de l’échantillon Écart-type de l’échantillon : STDEV. |
| Fonctions Python | Fonction numpy.std() : – Set : set ddof=0 – Set samples ddof=1 |
| Description du concept. | L’écart-type (σ) mesure la variance des données par rapport à la moyenne. – Faible écart-type : les points de données sont concentrés autour de la moyenne. – Écart-type élevé : les points de données sont plus dispersés. |
| Représentation visuelle. | Courbe graphique montrant un écart-type élevé et un écart-type faible. |
| Exemple de calcul. | La taille moyenne d’une classe d’élèves est de 75 pouces : – Points de données 56, 65, 74, 75, 75, 76, 77, 80, 81, 91. – Moyenne (µ) : 75 pouces |
| Étapes du calcul | 1) Soustraire la moyenne de chaque point de données. 2. Élever le résultat au carré 3. additionner les résultats au carré 4. Diviser par le nombre total de points de données. 6. Prendre la racine carrée |
| Données statistiques. | – 68 % à 75 ± 9,3 pouces de hauteur (1 écart-type) – 95 % à 75 ± 18,6 pouces (2 écarts types) – 99,7 % à 75 ± 27,9 pouces (3 écarts types) |
