Keine Ergebnisse gefunden
Wir konnten mit diesem Begriff nichts finden. Bitte versuche, nach etwas anderem zu suchen.
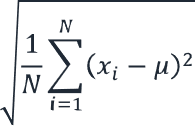
Standardabweichung (Statistik)
Mit diesem kostenlosen Online-Rechner für Standardabweichungen erhalten Sie schnelle und genaue Ergebnisse. Berechnen Sie die Gesamtstandardabweichung und die Stichprobenstandardabweichung, lernen Sie die wichtigsten Formeln kennen und sehen Sie Beispiele. Folgen Sie unserer schrittweisen Anleitung zur Berechnung von Varianz und Standardabweichung in Excel oder Python.
Bei Ihrer Berechnung ist ein Fehler aufgetreten.
| Ergebnis | |
|---|---|
| Standardabweichung | s = 4.5 |
| Abweichung | s2 = 20.24 |
| Zählen | n = 7 |
| Bedeuten | x̄ = 14.29 |
| Summe der Quadrate | SS = 100 |
| Felder | Einzelheiten |
|---|---|
| Definition | Die Standardabweichung ist ein Maß für den Grad der Streuung der Werte in einem Datensatz und gibt an, wie stark die Datenpunkte vom Mittelwert abweichen. |
| Typen | 1 . Gesamtstandardabweichung 2 . Stichproben-Standardabweichung |
| Gesamt-Standardabweichung | Formel: σ = √(1/N ∑(xi – μ)²) Wobei σ = Standardabweichung der Grundgesamtheit N = Anzahl der Datenpunkte xi = jeder Datenpunkt μ = Gesamtmittelwert |
| Standardabweichung der Stichprobe | Formel S = √(1/(n-1) ∑(xi – x̄)²) Wobei S = Standardabweichung der Stichprobe n = Anzahl der Datenpunkte in der Stichprobe x ̄ = Mittelwert der Stichprobe |
| Excel-Funktionen | – Standardabweichung der Grundgesamtheit: STDEV.P – Standardabweichung der Stichprobe Standardabweichung der Stichprobe: STDEV. |
| Python-Funktion | Funktion numpy.std() : – Einrichtung: Einrichtung ddof=0 – Stichprobe definieren ddof=1 |
| Konzeptualisierung. | Die Standardabweichung (σ) misst die Abweichung der Daten vom Mittelwert. – Geringe Standardabweichung: Die Datenpunkte sind um den Mittelwert konzentriert. – Hohe Standardabweichung: Die Datenpunkte sind stärker gestreut. |
| Visuelle Darstellung. | Ein Diagramm mit hoher und niedriger Standardabweichung. |
| Berechnungsbeispiel. | Die durchschnittliche Körpergröße der Schüler in einer Klasse beträgt 75 Zoll: – Datenpunkte 56, 65, 74, 75, 76, 77, 80, 81, 91. – Mittelwert (µ): 75 Zentimeter |
| Berechnungsschritte | 1) Ziehen Sie den Mittelwert von jedem Datenpunkt ab. 2) Quadriere das Ergebnis. 3) Addiere das Ergebnis zum Quadrat. 4) Dividiere durch die Gesamtzahl der Datenpunkte. 6) Ermitteln Sie die Quadratwurzel. |
| Statistische Daten. | – 68% (1 Standardabweichung) bei 75 ± 9,3 Zoll – 95% (2 Standardabweichungen) bei 75 ± 18,6 Zoll – 99,7% bei 75 ± 27,9 Zoll (3 Standardabweichungen) |
