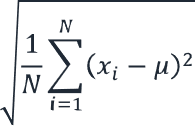
Standaardafwijking (statistiek)

Deze gratis online calculator voor standaardafwijkingen geeft je snelle en nauwkeurige resultaten. Bereken de totale standaardafwijking en de standaardafwijking van de steekproef, leer de belangrijkste formules en bekijk voorbeelden. Volg onze stap-voor-stap handleiding voor het berekenen van variantie en standaardafwijking in Excel of Python.

Gegevensset

Door komma's gescheiden getallen

Groep

Er is een fout opgetreden in uw berekening.

Resultaat
Standaarddeviatie	s = 4.5
Variantie	s² = 20.24
Tellen	n = 7
Bedoelen	x̄ = 14.29
Som van kwadraten	SS = 100

Velden	Details veld
Definitie	De standaardafwijking is een maat voor de mate van spreiding van de waarden in een gegevensverzameling en geeft aan hoeveel de gegevenspunten afwijken van de gemiddelde waarde.
Soorten	1 . Totale standaardafwijking 2 . Standaardafwijking steekproef
Totale standaardafwijking	Formule: σ = √(1/N ∑(xi – μ)²) Waarbij σ = standaardafwijking van de populatie N = aantal gegevenspunten xi = elk gegevenspunt μ = totale gemiddelde waarde
Standaardafwijking van de steekproef	Formule S = √(1/(n-1) ∑(xi – x̄)²) Waarbij S = standaardafwijking van de steekproef n = aantal meetpunten in de steekproef x ̄ = gemiddelde waarde van de steekproef
Excel-functies	– Standaardafwijking van de populatie: STDEV.P – Standaardafwijking van de steekproef Standaardafwijking van de steekproef: STDEV.
Python functie	Functie numpy.std() : – Setup: Setup ddof=0 – Monster definiëren ddof=1
Conceptualisatie.	De standaardafwijking (σ) meet de afwijking van de gegevens van het gemiddelde. – Lage standaardafwijking: De gegevenspunten zijn geconcentreerd rond het gemiddelde. – Hoge standaardafwijking: De gegevenspunten liggen meer verspreid.
Visuele weergave.	Een diagram met hoge en lage standaarddeviatie.
Rekenvoorbeeld.	De gemiddelde lengte van de leerlingen in een klas is 75 inch: – Datapunten 56, 65, 74, 75, 76, 77, 80, 81, 91. – Gemiddelde waarde (µ): 75 centimeter
Berekeningsstappen	1) Trek het gemiddelde van elk gegevenspunt af. 2) Kwadrateer het resultaat. 3) Tel het resultaat in het kwadraat op. 4) Deel door het totaal aantal datapunten. 6) Bepaal de vierkantswortel.











Statistische gegevens.	– 68% (1 standaardafwijking) bij 75 ± 9,3 inch – 95% (2 standaardafwijkingen) bij 75 ± 18,6 inch – 99,7% bij 75 ± 27,9 inch (3 standaardafwijkingen)