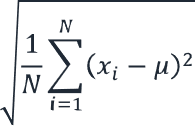
Deviazione standard (statistica)

La nostra calcolatrice online gratuita della deviazione standard fornisce risultati rapidi e precisi. Calcolate la deviazione standard totale e la deviazione standard del campione, imparate le formule di base e visualizzate gli esempi. Seguite la nostra guida passo passo per calcolare la varianza e la deviazione standard in Excel o Python.

Set di dati

Numeri separati da virgole

Gruppo

Si è verificato un errore nel calcolo.

Risultato
Deviazione standard	s = 4.5
Varianza	s² = 20.24
Contare	n = 7
Significare	x̄ = 14.29
Somma dei quadrati	SS = 100

Campi	Area di dettaglio
Descrizione	La deviazione standard è una misura del grado di dispersione dei valori in un insieme di dati e mostra quanto i punti di dati differiscono dal valore medio.
Tipi	1 . Deviazione standard complessiva 2 . Deviazione standard del campione
Deviazione standard totale	Equazione: σ = √(1/n ∑(∑(xi – μ)²) Dove è σ = deviazione standard della popolazione N = numero di punti dati xi = ogni punto dati μ = valore medio complessivo
Deviazione standard del campione	Formula S = √(1/(n-1)∑(xi – x̄)²) Dove è S = deviazione standard del campione n = numero di punti di misura nel campione x̄ = valore medio del campione
Funzioni di Excel	– Deviazione standard della popolazione: STDEV.P – Deviazione standard del campione Deviazione standard del campione Deviazione standard del campione Deviazione standard del campione Deviazione standard del campione: STDEV.
Funzione Python	Funzione numpy.std(): – Impostazione: Impostazione ddof=0 – Esempio di definizione ddof=1
Percezione.	La deviazione standard (σ) misura la deviazione dei dati dalla media. – Deviazione standard bassa: I punti dei dati sono centrati intorno alla media. – Deviazione standard alta: I punti dei dati sono più sparsi.
Rappresentazione visiva.	Grafico della deviazione standard alta e bassa.
Esempio matematico.	L’altezza media degli studenti di una classe è di 75 pollici: – Punti dati 56, 65, 65, 64, 74, 75, 75, 75, 76, 77, 80, 81, 91. – Valore medio (µ): 75 pollici
Fasi del calcolo	1) Sottrarre la media da ciascun punto dati. 2) Elevare il risultato al quadrato. 3) Somma il quadrato del risultato. 4) Dividere per il numero totale di punti dati. 6) Determinare la radice quadrata.











Statistiche	– 68% a 75 ± 9,3 pollici (1 deviazione standard) – 95% a 75 ± 18,6 pollici (2 deviazioni standard) – 99,7% a 75 ± 27,9 pollici (3 deviazioni standard)