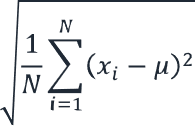
Standard eltérés (statisztika)

Ingyenes online szórásszámító kalkulátorunk gyors és pontos eredményeket biztosít. Számítsa ki a teljes szórást és a minta szórását, ismerje meg az alapvető képleteket és nézzen meg példákat. Kövesse lépésről lépésre útmutatóinkat a szórás és a szórás kiszámításához Excelben vagy Pythonban.

Adatkészlet

Vesszővel elválasztott számok

Csoport

Hiba történt a számításban.

Eredmény
Szórás	s = 4.5
Eltérés	s² = 20.24
Gróf	n = 7
Jelent	x̄ = 14.29
Négyzetek összege	SS = 100

Mezők	Részletezési terület
Leírás	A szórás az adathalmazban lévő értékek szóródásának mértékét mutatja, és azt mutatja, hogy az adatpontok mennyire térnek el az átlagértéktől.
Típusok	1 . Teljes szórás 2 . Minta szórás
Teljes szórás	Egyenlet: σ = √(1/n ∑(xi – μ)²) Ahol σ = a populáció szórása N = az adatpontok száma xi = az egyes adatpontok μ = teljes átlagérték
Minta szórás	Képlet S = √(1/(n-1)∑(xi – x̄)²) Ahol is S = a minta szórása n = a mérési pontok száma a mintában x̄ = a minta átlagértéke
Excel-funkciók	– A populáció szórása: STDEV.P – Minta szórás Minta szórás Minta szórás Minta szórás Minta szórás Minta szórás Minta szórás Minta szórás: STDEV.
Python függvény	Numpy.std() függvény: – ddof=0. – Meghatározási példa ddof=1
Érzékelés.	A szórás (σ) az adatok átlagtól való eltérését méri. – Alacsony szórás: Az adatpontok az átlag körül vannak központosítva. – Nagy szórás: Az adatpontok jobban szétszóródnak.
Vizuális ábrázolás.	A magas és alacsony szórás grafikonja.
Matematikai példa.	Egy osztályban a tanulók átlagos magassága 75 hüvelyk: – Az adatpontok 56, 65, 64, 74, 75, 75, 75, 76, 77, 80, 81, 91. – Középérték (µ): 75 hüvelyk
Számítási lépések	1) Vonjuk ki az átlagot minden egyes adatpontból. 2) Négyzetelje az eredményt. 3) Adjuk össze az eredmény négyzetét. 4) Osszuk el az adatpontok teljes számával. 6) Határozza meg a négyzetgyökét.











Statisztika	– 68% 75 ± 9,3 hüvelyk (1 standard eltérés) esetén – 95% 75 ± 18,6 hüvelyknél (2 standard eltérés) – 99,7% a 75 ± 27,9 hüvelyk (3 standard eltérés) esetén