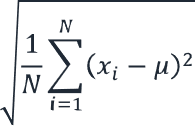
Směrodatná odchylka (statistická)

Naše bezplatná online kalkulačka odchylky poskytuje rychlé a přesné výsledky. Vypočítejte celkovou a výběrovou variance, naučte se základní vzorec a prohlédněte si příklady. Postupujte podle našich pokynů krok za krokem a vypočítejte směrodatnou odchylku a rozptyl v aplikaci Excel nebo Python.

Datový soubor

Čísla oddělená čárkami

Skupina

Ve vašem výpočtu se vyskytla chyba.

Výsledek
Směrodatná odchylka	s = 4.5
Odchylka	s² = 20.24
Počítat	n = 7
Znamenat	x̄ = 14.29
Součet čtverců	SS = 100

Pole	Podrobnosti o poli
Popis	Směrodatná odchylka je míra rozptylu hodnot v souboru dat a udává, jak moc se datové body odchylují od střední hodnoty.
Typy	1 . Celková odchylka 2 . výběrová odchylka
Celková odchylka	Rovnice: σ = √(1/n ∑(xi – μ)²) Kde σ = populační rozptyl N = počet datových bodů xi = počet datových bodů μ = celková střední hodnota
Směrodatná odchylka vzorku	Vzorec S = √(1/(n-1)∑(xi – x̄)²) Kde také S = směrodatná odchylka vzorku n = počet bodů měření ve vzorku x̄ = střední hodnota vzorku
Funkce aplikace Excel	– Směrodatná odchylka populace: STDEV.P – Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku Standardní odchylka vzorku: STDEV.
Funkce Pythonu	Funkce numpy.std(): – ddof = 0. – Příklad definice ddof = 1
Vnímání	Směrodatná odchylka (σ) měří odchylku dat od průměru. – Nízká odchylka: datové body jsou soustředěny kolem průměru. – Vysoká odchylka: Datové body jsou více rozptýlené.
Vizuální znázornění.	Grafy s vysokou a nízkou odchylkou.
Matematický příklad.	Průměrná výška žáků ve třídě je 75 palců: – Datové body jsou 56, 65, 64, 74, 75, 75, 75, 75, 75, 76, 77, 80, 81, 91. – Průměr (µ): 75 palců
Kroky výpočtu	1) Od každého datového bodu odečtěte průměr. 2) Výsledek odmocněte. 3) Sečtěte čtverce výsledků. 4) Vydělte celkovým počtem datových bodů. 5) Určete druhou odmocninu ze čtverce. 6) Určete druhou odmocninu ze čtverce.











Statistika	– 68 % pro 75 ± 9,3 palce (1 směrodatná odchylka). – 95 % pro 75 ± 18,6 palců (2 směrodatné odchylky) – 99,7 % pro 75 ± 27,9 palců (3 směrodatné odchylky)