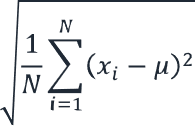
Deviasi standar (statistik)

Kalkulator varians online gratis kami memberikan hasil yang cepat dan akurat. Hitung varians total dan varians sampel, pelajari rumus dasar, dan lihat contohnya. Ikuti petunjuk langkah demi langkah kami untuk menghitung deviasi standar dan varians di Excel atau Python.

Kumpulan Data

Angka yang dipisahkan koma

Kelompok

Ada kesalahan dengan perhitungan Anda.

Hasil
Standar Deviasi	s = 4.5
Varians	s² = 20.24
Hitung	n = 7
Berarti	x̄ = 14.29
Jumlah Kuadrat	SS = 100

Bidang	Bidang detail
Deskripsi	Deviasi standar adalah tingkat penyebaran nilai dalam kumpulan data dan menunjukkan seberapa jauh titik data menyimpang dari nilai rata-rata.
Jenis	1 . Varians total 2 . varians sampel
Varians total	Persamaan: σ = √(1/n ∑(xi – μ)²) Dimana σ = varians populasi N = jumlah titik data xi = jumlah titik data μ = nilai rata-rata keseluruhan
Simpangan baku sampel	Rumus S = √(1/(n-1)∑(xi – x̄)²) Di mana juga S = deviasi standar sampel n = jumlah titik pengukuran dalam sampel x̄ = nilai rata-rata sampel
Fungsi Excel	– Standar deviasi populasi: STDEV.P – Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel Simpangan baku sampel: STDEV.
Fungsi Python	Fungsi numpy.std (): – ddof = 0. – Contoh definisi ddof = 1
Persepsi	Standar deviasi (σ) mengukur deviasi data dari rata-rata. – Varians rendah: Titik data terpusat di sekitar rata-rata. – Varians tinggi: Titik-titik data lebih tersebar.
Representasi visual.	Grafik varians tinggi dan rendah.
Contoh matematika.	Tinggi rata-rata siswa di kelas adalah 75 inci: – Titik data adalah 56, 65, 64, 74, 75, 75, 75, 76, 77, 80, 81, 91. – Rata-rata (µ): 75 inci
Langkah-langkah perhitungan	1) Kurangi rata-rata dari setiap titik data. 2) Kuadratkan hasilnya. 3) Tambahkan kuadrat hasilnya. 4) Bagilah dengan jumlah total titik data. 6) Tentukan akar kuadrat dari kuadrat tersebut.











Statistik	– 68% untuk 75 ± 9,3 inci (1 standar deviasi) – 95% pada 75 ± 18,6 inci (2 standar deviasi) – 99,7% untuk 75 ± 27,9 inci (3 deviasi standar)