結果は見つかりませんでした
その言葉を使ったものは見つかりませんでした。他の言葉で検索してみてください。
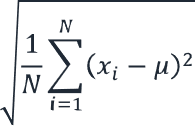
標準偏差
この無料のオンライン標準偏差電卓で迅速かつ正確な結果を得る。母集団と標本の標準偏差を計算し、主要な数式を学び、例を探る。簡単にステップバイステップのガイドでExcelやPythonで分散と標準偏差を計算します。
計算に誤りがありました。
| 結果 | |
|---|---|
| 標準偏差 | s = 4.5 |
| 分散 | s2 = 20.24 |
| 数える | n = 7 |
| 意味する | x̄ = 14.29 |
| 平方和 | SS = 100 |
| セクション | 詳細 |
|---|---|
| 定義 | 標準偏差は、データセット内の値の分散を表す尺度であり、あるデータ点が平均値からどれだけ乖離しているかを示す。 |
| 種類 | 1.母集団の標準偏差 2.標本の標準偏差 |
| 母集団の標準偏差 | 式: σ = √(1/N ∑(xi – μ)²) ここで σ = 母集団標準偏差 N = データ点の数 xi = 各データ点 μ = 母集団の平均 |
| 標本の標準偏差 | 式: s = √(1/(n-1) ∑(xi – x̄)²) ここで s = 標本の標準偏差 n = サンプル中のデータ点の数 x ̄ = 標本の平均 |
| Excel関数 | – 母集団の標準偏差:STDEV.P – 標本の標準偏差標本の標準偏差:STDEV.S |
| Python関数 | numpy.std() 関数を使用します: – 母集団:ddof=0を設定 – サンプルddof=1に設定 |
| 概念の説明 | 標準偏差(σ)は平均に対するデータの分散を測定する。 – 標準偏差が低い:データ点が平均値の周りに集まっている。 – 標準偏差が高い:データ点がより分散している。 |
| 視覚的表現 | 高標準偏差と低標準偏差を示すグラフ曲線。 |
| 計算例 | 平均身長75インチのクラスの場合: – データポイント56, 65, 74, 75, 76, 77, 80, 81, 91 – 平均 (μ):75インチ |
| 計算手順 | 1.各データポイントから平均を引く 2.結果を二乗する 3.二乗した結果を合計する 4.データ点の総数で割る 5.平方根をとる |
| 統計的洞察 | – 高さの68%が75±9.3インチ以内(1標準偏差) – 95%が75±18.6インチ以内(2標準偏差) – 99.7%が75±27.9インチ以内(3標準偏差) |
