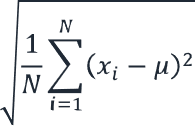
표준 편차(통계)

이 무료 온라인 표준편차 계산기로 빠르고 정확한 결과를 얻으세요. 전체 표준 편차와 샘플 표준 편차를 계산하고, 주요 공식을 배우고, 예제를 살펴보세요. 단계별 가이드를 따라 Excel 또는 Python에서 분산과 표준 편차를 계산하세요.

데이터 세트

쉼표로 구분된 숫자

그룹

계산에 오류가 있습니다.

결과
표준 편차	s = 4.5
분산	s² = 20.24
세다	n = 7
의미하다	x̄ = 14.29
제곱합	SS = 100

분야	세부 정보
정의	표준 편차는 데이터 세트의 값 분산 정도를 측정하는 척도로, 데이터 포인트가 평균에서 벗어나는 정도를 나타냅니다.
유형	1 . 전체 표준 편차 2 . 샘플 표준 편차
전체 표준 편차	공식: σ = √(1/N ∑(xi – μ)²) 여기서 σ = 전체 모집단의 표준 편차 N = 데이터 포인트 수 xi = 각 데이터 포인트 μ = 전체 평균
샘플 표준 편차	공식 S = √(1/(n-1) ∑(xi – x̄)²) 여기서 s = 샘플 표준 편차 n = 샘플의 데이터 포인트 수 x ̄ = 샘플 평균
Excel 함수	– 모집단의 표준 편차: STDEV.P – 표본 표준 편차 표본 표준 편차: STDEV.
Python 함수	함수 numpy.std() : – 설정: 설정 ddof=0 – 샘플 ddof=1 정의
개념 설명.	표준 편차(σ)는 평균으로부터 데이터의 변화를 측정합니다. – 낮은 표준 편차: 데이터 포인트가 평균 주위에 집중되어 있습니다. – 높은 표준 편차: 데이터 포인트가 더 분산되어 있습니다.
시각적 표현.	높은 표준 편차와 낮은 표준 편차를 보여주는 그래프입니다.
계산 예제.	한 학급 학생의 평균 키는 75인치입니다: – 데이터 포인트 56, 65, 74, 75, 76, 77, 80, 81, 91. – 평균(µ): 75인치
계산 단계	1) 각 데이터 포인트에서 평균을 뺍니다. 2. 결과를 제곱합니다. 3) 결과를 제곱에 더합니다. 4. 총 데이터 포인트 수로 나눕니다. 6. 제곱근을 구합니다.











통계 데이터.	– 75 ± 9.3인치에서 68%(1표준편차) – 75 ± 18.6인치에서 95%(2표준편차) – 75 ± 27.9인치에서 99.7%(표준편차 3개)